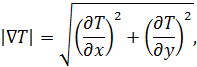Шумопонижение — процесс устранения шумов из полезного сигнала с целью повышения его субъективного качества. В изображениях подавление шума используется для лучшего визуального восприятия человеком или как один из этапов предобработки для последующего анализа. Существует множество алгоритмов шумопонижения, например, линейное усреднение пикселей, математическая морфология и др.
В этой статье рассмотрим метод подавления шума, в основе которого лежит уравнение теплопроводности (диффузии). Идея метода и реализация предложены в работе [1].
Предположим, что имеется зашумленное черно-белое изображение. Будем интерпретировать яркость пикселя, которая задаётся целым числом от 0 до 255, как температуру (или концентрацию вещества) в данной точке, а изображение на входе, как распределение температур в начальный момент времени в тонкой прямоугольной мембране. В условиях теплоизоляции такой мембраны, температура в ней со временем будет выравниваться, а области, соответствующие шуму, будут подвержены этому эффекту наиболее интенсивно. Это хорошо видно на следующей анимации, где температура точки передаётся её высотой и цветом. Большой круг в центре теряет тепло медленно, а точка слева — быстро.

Таким образом, если остановить процесс в нужное время, то шум станет значительно слабее, а само изображение ещё не успеет заметно исказиться.
Ниже приведем алгоритм в действии. Пусть исходное изображение содержит основной объект (круг) и шум (белую точку),

тогда, применив к нему уравнение теплопроводности (диффузии), получим

Код в MATLAB
T = imread(‘1.png’); % чтение изображения из файла
T = rgb2gray(T); % перевод изображения в черно-белое
[m, n] = size(T);
XX = linspace(1, m, m);
YY = linspace(1, n, n);
[X, Y] = meshgrid(XX, YY); % создание сетки
CFL = 0.125; % Критерий Куранта — Фридрихса — Леви
dx = XX(2) — XX(1); % приращение пространственных переменных
dt = CFL*dx^2; % приращение времени
imshow(T); % вывод изображения в начальный момент времени
title(strcat(‘Время t =’, sprintf(‘ %.1f’, 0)));
Z = T;
for t = dt:dt:2.5
for i = 2:(m-1)
for j = 2:(n-1)
% численное решение уравнения теплопроводности
Z(i, j) = T(i, j) + dt*(T(i+1, j) + T(i-1, j) + …
T(i, j-1) + T(i, j+1) — 4*T(i, j))/dx^2;
end
end
T = Z;
T = uint8(round(T));
imshow(T); % вывод текущего изображения
title(strcat(‘Время t =’, sprintf(‘ %.1f’, t)));
pause(0.05);
T = double(T);
end
Идея этого кода базируется на использовании уравнения теплопроводности следующего вида
где ![]() — температура точки
— температура точки ![]() в момент времени
в момент времени ![]() ,
, ![]() — оператор Лапласа. Для численного решения производные в уравнении были заменены конечными разностями:
— оператор Лапласа. Для численного решения производные в уравнении были заменены конечными разностями:
Следует отметить существенный недостаток предложенного алгоритма — размытие кромок объектов, и как следствие — потерю чёткости изображения. Поэтому далее будет предложен модифицированный алгоритм.
Кромки объектов можно определять с помощью модуля градиента:
где
Если модуль градиента вывести как изображение, то получим

т.е. на кромках величина градиента значительно больше, чем в остальных точках, поэтому на изображении кромки светлые, а всё остальное — ближе к черному.
Код в MATLAB
T = imread(‘1.png’); % чтение изображения из файла
T = rgb2gray(T); % перевод изображения в черно-белое
[m, n] = size(T);
XX = linspace(1, m, m);
YY = linspace(1, n, n);
[X, Y] = meshgrid(XX, YY); % создание сетки
T = double(T);
u = T;
for i = 2:(m-1)
for j = 2:(n-1)
% вычисление градиента
u(i, j) = sqrt((T(i+1,j)-T(i-1,j))^2+(T(i,j+1)-T(i,j-1))^2)/4;
end
end
u = uint8(round(u));
imshow(u); % вывод изображения
Чтобы иметь возможность управлять процессом теплопередачи вблизи кромок, перейдем к уравнению теплопроводности в более общей форме:
где ![]() — коэффициент теплопроводности,
— коэффициент теплопроводности, ![]() — плотность,
— плотность, ![]() — теплоемкость,
— теплоемкость, ![]() — градиент температуры
— градиент температуры ![]() .
.
Будем полагать, что ![]() . Если положить
. Если положить ![]() , то получим уравнение вида (1). Мы же потребуем, чтобы коэффициент
, то получим уравнение вида (1). Мы же потребуем, чтобы коэффициент ![]() зависел от величины градиента
зависел от величины градиента ![]() , причем так, чтобы
, причем так, чтобы ![]() при
при ![]() , т. е. коэффициент теплопроводности должен быть тем ближе к нулю, чем больше величина градиента. Тогда перенос тепла вблизи кромок будет минимальным, и размытия кромок не произойдет, а ровные шумные области, наоборот, будут хорошо сглажены.
, т. е. коэффициент теплопроводности должен быть тем ближе к нулю, чем больше величина градиента. Тогда перенос тепла вблизи кромок будет минимальным, и размытия кромок не произойдет, а ровные шумные области, наоборот, будут хорошо сглажены.
На роль функции ![]() можно подобрать множество кандидатов, например, в работе [1] были предложены
можно подобрать множество кандидатов, например, в работе [1] были предложены
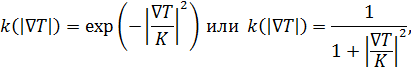 где константа
где константа ![]() позволяет регулировать чувствительность алгоритма и подбирается опытным путем. Пусть далее
позволяет регулировать чувствительность алгоритма и подбирается опытным путем. Пусть далее
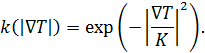 Так как коэффициент теплопроводности в нашем случае зависит от градиента, а значит зависит от
Так как коэффициент теплопроводности в нашем случае зависит от градиента, а значит зависит от ![]() и
и ![]() , то дивергенцию, входящую в уравнение (2), можно расписать следующим образом:
, то дивергенцию, входящую в уравнение (2), можно расписать следующим образом:
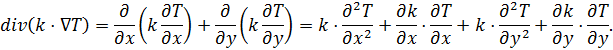 Выполним переход от непрерывного уравнения (2) к дискретному
Выполним переход от непрерывного уравнения (2) к дискретному
![]()
![]()
![]()
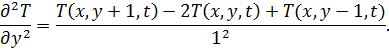
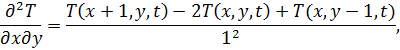
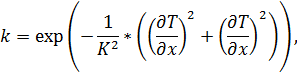
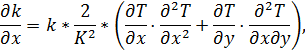
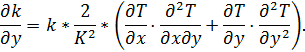 Ниже приводится анимация работы алгоритма, основанного на уравнении (2), с шумом типа «соль и перец»:
Ниже приводится анимация работы алгоритма, основанного на уравнении (2), с шумом типа «соль и перец»:

Код в MATLAB
T = imread(‘2.png’); % чтение изображения из файла
T = rgb2gray(T); % перевод изображения в черно-белое
[m, n] = size(T);
XX = linspace(1, m, m);
YY = linspace(1, n, n);
[X, Y] = meshgrid(XX, YY); % создание сетки
CFL = 0.125; % Критерий Куранта — Фридрихса — Леви
dx = XX(2) — XX(1); % приращение пространственных переменных
dt = CFL*dx^2; % приращение времени
subplot 121, imshow(T,[]);
title(strcat(‘Время t =’, sprintf(‘ %.1f’, 0)));
Z = T;
K = 10; % регулирует чувствительность
T = double(T);
% численное решение
for t = dt:dt:1
for i = 2:(m-1)
for j = 2:(n-1)
T_x = (T(i+1,j) — T(i-1,j))/2;
T_y = (T(i,j+1) — T(i,j-1))/2;
T_xx = T(i+1,j) — 2*T(i,j) + T(i-1,j);
T_yy = T(i,j+1) — 2*T(i,j) + T(i,j-1);
T_xy = T(i+1,j) — 2*T(i,j) + T(i,j-1);
k = exp(-1/K^2*(T_x^2 + T_y^2));
k_x = k*2/K^2*(T_x*T_xx + T_y*T_xy);
k_y = k*2/K^2*(T_x*T_xy + T_y*T_yy);
Z(i, j) = T(i, j) + dt*(k*(T_xx+T_yy)+k_x*T_x+k_y*T_y);
end
end
T = Z;
% вывод текущего изображения
T = uint8(round(T));
subplot 122, imshow(T,[])
title(strcat(‘Время t =’, sprintf(‘ %.1f’, t)));
pause(0.05);
T = double(T);
end
В конце отметим, что алгоритм не является универсальным и имеет свои недостатки, к числу которых можно отнести и медленную скорость работы. Но все же приведенный пример показывает, что предложенный алгоритм со своей задачей справляется.
Литература
- Perona and J. Malik. Scale-space and edge detection using anisotropic diffusion. IEEE Trans. Pattern Anal. Machine Intell., vol. 12, pp. 629–639, 1990.
- https://en.wikipedia.org/wiki/Anisotropic_diffusion
- https://habrahabr.ru/post/144288/
- http://cgm.computergraphics.ru/content/view/74#